Vztah funkcí celkových a mezních

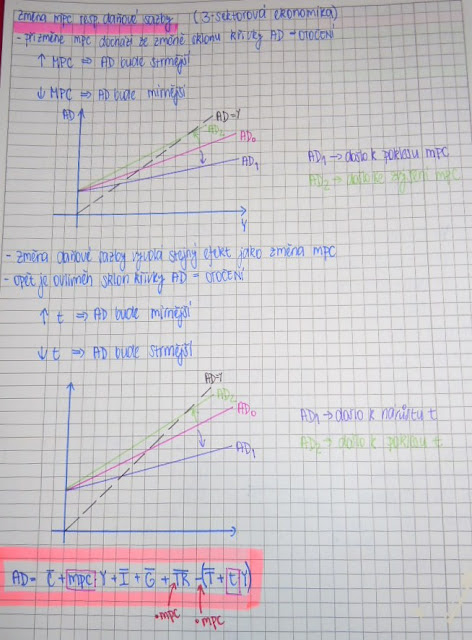
Která z křivek znázorňující Mf je správná???

Hledání extrémů funkcí dvou proměnných

Zopakuj si teorii pro hledání extrémů funkce dvou reálných proměnných

• (a) bez vazby, 
• (b) s vazbou
• extrémy funkcí jsou jednou z nejdůležitějších aplikací diferenciálního počtu

Pokles daňové sazby

• Ekonomika je dána těmito parametry: Důchod je 1000, mpc = 0,8, sazba důchodové daně se změní z 0,3 na 0,2.
• Popište rovnicemi AD před změnou a po změně.
• Danou změny AD zakreslete. Zobrazte změnu rovnovážné úrovně důchodu.
• Změnu důchodu kvantifikujte.
• O kolik se změní daňové příjmy vlády?

Spotřeba ve třísektorové ekonomice

• Je dána spotřební funkce C = 200 + 0,8 YD (disponibilní důchod).
• Investice jsou ve výši 100, vládní výdaje jsou 300, transferové platby 125, autonomní daně 100 a daňová sazba 0,25.
• Jaká je velikost multiplikátoru?
• Jaká je velikost celkové spotřeby?

Změna kvality vládních výdajů

• V ekonomice dojde ke snížení transferových plateb a současně ke zvýšení vládních nákupů zboží a služeb o stejný objem.
• Odvoďte teoreticky, jaký vliv má přesun na úroveň rovnovážného důchodu (modelujte rovnováhu před, resp. po změně; odečtěte). 
• Své úvahy ověřte výpočtem pro mpc = 0,8; t = 0,2; přesun vládních výdajů z položky transfery na vládní nákupy zboží a služeb je 50 jednotek. Jaká je změna rovnovážného důchodu.
• Na základě získaných znalostí popište současné intervence vlády a jejich důsledky (citujte z tisku a komentujte).

Změna mpc resp. daňové sazby

• Modelujte účinky změn mezního sklonu ke spotřebě, resp. změn daňové sazby (ve třísektorové ekonomice). 
• Popisujte a zakreslete.

Dvousektorová ekonomika

• Předpokládejme, že GNP = 1000 jednotek, přičemž C = 800 a I = 200, mpc = 0,5.
• Firma se rozhodne postavit sklad a její investice se zvýší z 200 na 210 jednotek.
• Popište přechod od staré rovnováhy k nové.
• Určete velikost přírůstku důchodu (odečtením dvou předchozích rovnic).
• Popište multiplikační účinek, tj. o kolik se zvýší GNP, když investice se zvýší o 10 jednotek.
• Zakreslete starou a novou rovnováhu, vyznačte změny I a GNP.
• Popište v obrázku multiplikační efekt.