Hodnocení výuky Matematika v ekonomii

K matematice v ekonomii pod vedením paní doktorky Bauerové neodmyslitelně patří blog a webové prostředí vůbec, proto jsem se rozhodla zhodnotit tento předmět, kde jinde než na svém vlastním blogu.

Takže ráda bych začala od naprostého začátku, tedy od první přednášky a od prvního cvičení. Již před první přednáškou jsem slyšela od některých spolužáků: "Představ si, že budeme muset mít nějaký blog a dělat na něm úkoly!!!" Docela jsem se vyděsila již před samotným prvním kontaktem s tímto předmětem a s paní doktorkou Bauerovou. Mé pocity se nijak nezměnily ani po prvním týdnu výuky. Bála jsem se množství učiva, bála jsem se, že nebudu dostatečně chápat propojení mezi matematikou a ekonomií a také mě dost děsil styl výuky. Styl výuky mě děsil především proto, že jsem nikdy nezakládala blog, nikdy jsem nespolupracovala po internetu se spolužáky tak organizovaně a bála jsem se, že moje znalost "blogování" nebude dostatečná. Nicméně jsem na nic nečekala a hned druhý týden jsem si založila gmail a také blog.

Do umění blogování jsem se rychle dostala a snažila se vždy prezentovat své úkoly právě na svém blogu. Ne vždy se mi to podařilo, nebo jsem někdy musela své řešení upravit či dokonce úplně změnit, ale musím říct, že mě to nakonec moc bavilo a vytváření blogu jsem si užila. Nakonec je pěkné se zpětně podívat na výsledky své práce, které jsou na blogu daleko přehlednější a patrnější než na různých papírech, které jsou dnes (již po úspěšném napsání SPP2) na dně papírové krabice :)

Během semestru jsem se snažila navštěvovat jak přednášky, tak cvičení. Přednášky mi dávaly hrozně moc, protože jsem během nich vždy pochopila spojitosti, které se nám paní doktorka Bauerová snažila přiblížit. Cvičení mi pak pomohly doplnit nedostatky úkolů, které jsme dostávaly zadané. Práce během semestru bylo přiměřeně a když člověk pracoval průběžně, to znamená, že dělal do matematiky úkoly každý týden, tak před SPP1 a SPP2 stačilo rychle projít všechny příklady a úspěch byl zaručen :)

Po 14 dní jsem byla nemocná a nenavštěvovala jsem školu, bylo příjemné vědět, že zbytečně nemusím obtěžovat své kamarádky, aby mi poskytly materiály. Materiály k samostudiu paní doktorky Bauerové mi pomohly plně pochopit látku a také vypracovat zadané úkoly.

Nakonec bych ráda subjektivně zhodnotila své znalosti. Musím říct, že mi matematika pomohla pochopit mnohé souvislosti v ekonomii a to především v makroekonomii v modelu IS-LM. Jelikož jsou cvičení z Makroekonomie B jednou za 14 dní, byla jsem za Matematiku v ekonomii v tomto semestru velmi vděčná. Moc mi pomohla!

Sama jsem si říkala, že bych ocenila takový přístup k výuce i u jiných předmětů :) Byla by to zajímavá změna!

Makroekonomická rovnováha v čase

Určete, jak se vyvíjí důchod v čase, je-li mpc = 0,6; autonomní C = 160; autonomní I = 40. Zpoždění mezi důchodem a poptávkou je o jedno období.

• Jaká je statická rovnováha? Také obecně.
• Zapiš rovnici zpožděné AD v jednosektorové ekonomice.
• ... ve dvousektorové.
• Jaký je vývoj důchodu v dlouhém období (řeš diferenční rovnici)?
• Urči vývoj důchodu pro počáteční podmínku důchod v čase nula = 600. 
• Situaci zakresli.
• Zapiš obecně, kam se blíží důchod v dlouhém období (limitou.)

Dynamický model S-D, zpoždění na straně poptávky

• Přehoď v modelu S-D (viz předchozí příklady) zpoždění na stranu poptávky, a to pro oba předchozí poměry sklonů S, resp. D.
• Řeš nejprve matematicky a pak teprve graficky. Zkontroluj pokaždé souhlas.
• Zapiš přehledně a systematicky všechny čtyři případy dynamické rovnováhy S-D pro nespojité změny.¨

Nekonvergentní nespojitý model S-D při zpoždění na straně nabídky

• Přehoď vzájemný poměr sklonů z předchozích příkladů.
• Vykonej všechny kroky z předchozích příkladů.
• Přehledně zapiš srovnání.

Početní určení konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období straně nabídky.
• Zapiš rovnice dynamické rovnováhy, tj. diferenční rovnici.
• Řeš rovnici ve všech bodech s matematickým popisem.
• Spočti také partikulární řešení odpovídající počáteční podmínce.
• Vypiš předpis (funkci), která charakterizuje vývoj cen v čase.
• Interpretuj řešení, tj. vytvoř tabulku hodnot nalezené funkce vývoje cen v čase.
• Zakresli vývoj cen v čase, resp. vývoj odchylek v čase (z hodnot v tabulce).
• Zkontroluj správnost porovnáním s grafickým řešením, resp. s intuitivním odhadem.
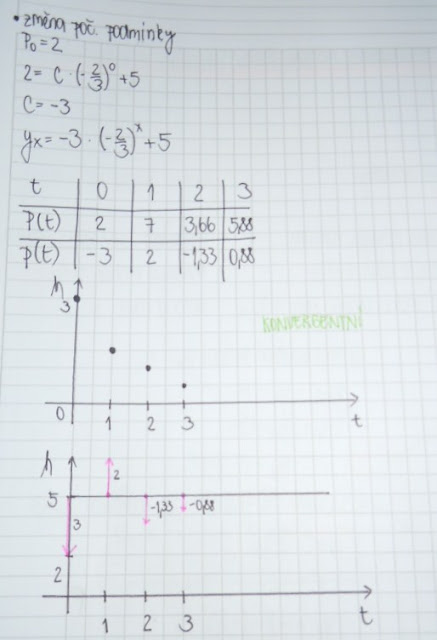
• Změň počáteční podmínku na počáteční cenu rovnu 2 jednotkám. Zakresli, popiš.
• Interpretuj, co znamená změna počáteční podmínky (dle grafu). 

Grafické určení a znázornění konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Zakresli S, D do přehledného grafu přesně v měřítku.
• Vyznač vývoj tlaků na změny ceny v čase, tj. zakresli "pavučinu" ke grafu S-D.
• Vyznač velikost odchylek od rovnovážné ceny na straně nabídky. Označ p0, p1, p2 atd.
• Zakresli graf vývoje odchylek, resp. absolutních hodnot odchylek v čase.
• Zakresli vývoj cen v čase.
• Zapiš limitu týkající se vývoje odchylek v čase a odpovídající konvergenci, resp. divergenci modelu.

Intuitivní odhad konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Odhadněte intuitivně (pomocí porovnání sklonů S, D), zda je model konvergentní, tj. zda situace spěje k rovnovážné ceně.
• Jedná se o model nespojitý nebo spojitý?