Určete, jak se vyvíjí důchod v čase, je-li mpc = 0,6; autonomní C = 160; autonomní I = 40. Zpoždění mezi důchodem a poptávkou je o jedno období.
- Jaká je statická rovnováha? Také obecně.
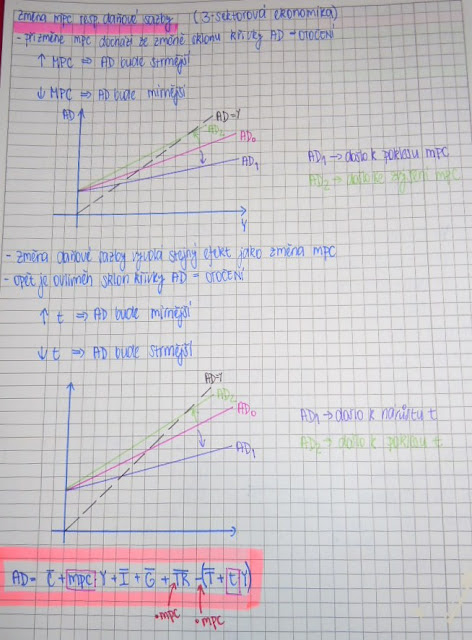
- Zapiš rovnici zpožděné AD v jednosektorové ekonomice.
- ... ve dvousektorové.
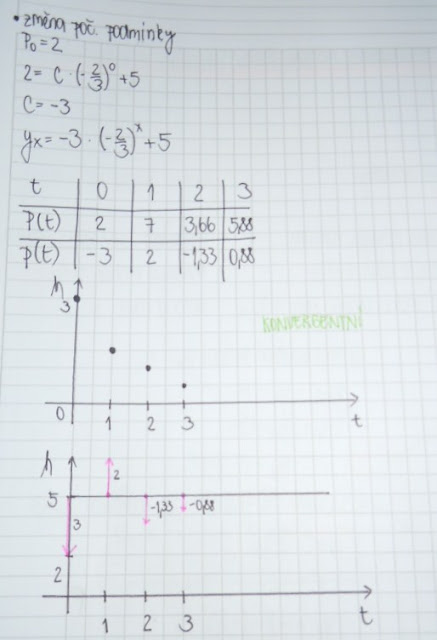
- Jaký je vývoj důchodu v dlouhém období (řeš diferenční rovnici)?
- Urči vývoj důchodu pro počáteční podmínku důchod v čase nula = 600.
- Situaci zakresli.
- Zapiš obecně, kam se blíží důchod v dlouhém období (limitou.)