Hodnocení výuky Matematika v ekonomii

K matematice v ekonomii pod vedením paní doktorky Bauerové neodmyslitelně patří blog a webové prostředí vůbec, proto jsem se rozhodla zhodnotit tento předmět, kde jinde než na svém vlastním blogu.

Takže ráda bych začala od naprostého začátku, tedy od první přednášky a od prvního cvičení. Již před první přednáškou jsem slyšela od některých spolužáků: "Představ si, že budeme muset mít nějaký blog a dělat na něm úkoly!!!" Docela jsem se vyděsila již před samotným prvním kontaktem s tímto předmětem a s paní doktorkou Bauerovou. Mé pocity se nijak nezměnily ani po prvním týdnu výuky. Bála jsem se množství učiva, bála jsem se, že nebudu dostatečně chápat propojení mezi matematikou a ekonomií a také mě dost děsil styl výuky. Styl výuky mě děsil především proto, že jsem nikdy nezakládala blog, nikdy jsem nespolupracovala po internetu se spolužáky tak organizovaně a bála jsem se, že moje znalost "blogování" nebude dostatečná. Nicméně jsem na nic nečekala a hned druhý týden jsem si založila gmail a také blog.

Do umění blogování jsem se rychle dostala a snažila se vždy prezentovat své úkoly právě na svém blogu. Ne vždy se mi to podařilo, nebo jsem někdy musela své řešení upravit či dokonce úplně změnit, ale musím říct, že mě to nakonec moc bavilo a vytváření blogu jsem si užila. Nakonec je pěkné se zpětně podívat na výsledky své práce, které jsou na blogu daleko přehlednější a patrnější než na různých papírech, které jsou dnes (již po úspěšném napsání SPP2) na dně papírové krabice :)

Během semestru jsem se snažila navštěvovat jak přednášky, tak cvičení. Přednášky mi dávaly hrozně moc, protože jsem během nich vždy pochopila spojitosti, které se nám paní doktorka Bauerová snažila přiblížit. Cvičení mi pak pomohly doplnit nedostatky úkolů, které jsme dostávaly zadané. Práce během semestru bylo přiměřeně a když člověk pracoval průběžně, to znamená, že dělal do matematiky úkoly každý týden, tak před SPP1 a SPP2 stačilo rychle projít všechny příklady a úspěch byl zaručen :)

Po 14 dní jsem byla nemocná a nenavštěvovala jsem školu, bylo příjemné vědět, že zbytečně nemusím obtěžovat své kamarádky, aby mi poskytly materiály. Materiály k samostudiu paní doktorky Bauerové mi pomohly plně pochopit látku a také vypracovat zadané úkoly.

Nakonec bych ráda subjektivně zhodnotila své znalosti. Musím říct, že mi matematika pomohla pochopit mnohé souvislosti v ekonomii a to především v makroekonomii v modelu IS-LM. Jelikož jsou cvičení z Makroekonomie B jednou za 14 dní, byla jsem za Matematiku v ekonomii v tomto semestru velmi vděčná. Moc mi pomohla!

Sama jsem si říkala, že bych ocenila takový přístup k výuce i u jiných předmětů :) Byla by to zajímavá změna!

Makroekonomická rovnováha v čase

Určete, jak se vyvíjí důchod v čase, je-li mpc = 0,6; autonomní C = 160; autonomní I = 40. Zpoždění mezi důchodem a poptávkou je o jedno období.

• Jaká je statická rovnováha? Také obecně.
• Zapiš rovnici zpožděné AD v jednosektorové ekonomice.
• ... ve dvousektorové.
• Jaký je vývoj důchodu v dlouhém období (řeš diferenční rovnici)?
• Urči vývoj důchodu pro počáteční podmínku důchod v čase nula = 600. 
• Situaci zakresli.
• Zapiš obecně, kam se blíží důchod v dlouhém období (limitou.)

Dynamický model S-D, zpoždění na straně poptávky

• Přehoď v modelu S-D (viz předchozí příklady) zpoždění na stranu poptávky, a to pro oba předchozí poměry sklonů S, resp. D.
• Řeš nejprve matematicky a pak teprve graficky. Zkontroluj pokaždé souhlas.
• Zapiš přehledně a systematicky všechny čtyři případy dynamické rovnováhy S-D pro nespojité změny.¨

Nekonvergentní nespojitý model S-D při zpoždění na straně nabídky

• Přehoď vzájemný poměr sklonů z předchozích příkladů.
• Vykonej všechny kroky z předchozích příkladů.
• Přehledně zapiš srovnání.

Početní určení konvergence v pavučinovém modelu S-D

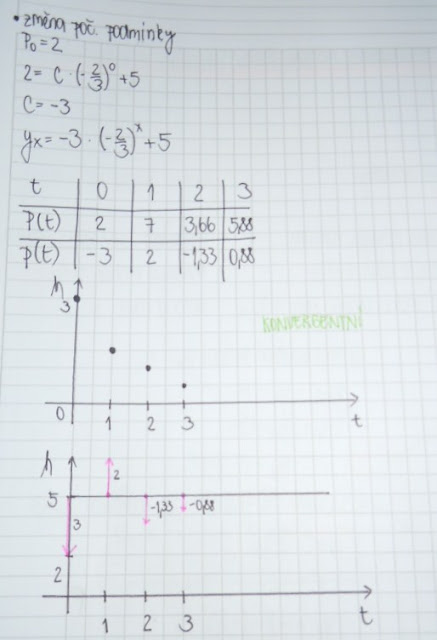
• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období straně nabídky.
• Zapiš rovnice dynamické rovnováhy, tj. diferenční rovnici.
• Řeš rovnici ve všech bodech s matematickým popisem.
• Spočti také partikulární řešení odpovídající počáteční podmínce.
• Vypiš předpis (funkci), která charakterizuje vývoj cen v čase.
• Interpretuj řešení, tj. vytvoř tabulku hodnot nalezené funkce vývoje cen v čase.
• Zakresli vývoj cen v čase, resp. vývoj odchylek v čase (z hodnot v tabulce).
• Zkontroluj správnost porovnáním s grafickým řešením, resp. s intuitivním odhadem.
• Změň počáteční podmínku na počáteční cenu rovnu 2 jednotkám. Zakresli, popiš.
• Interpretuj, co znamená změna počáteční podmínky (dle grafu). 

Grafické určení a znázornění konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Zakresli S, D do přehledného grafu přesně v měřítku.
• Vyznač vývoj tlaků na změny ceny v čase, tj. zakresli "pavučinu" ke grafu S-D.
• Vyznač velikost odchylek od rovnovážné ceny na straně nabídky. Označ p0, p1, p2 atd.
• Zakresli graf vývoje odchylek, resp. absolutních hodnot odchylek v čase.
• Zakresli vývoj cen v čase.
• Zapiš limitu týkající se vývoje odchylek v čase a odpovídající konvergenci, resp. divergenci modelu.

Intuitivní odhad konvergence v pavučinovém modelu S-D

• Mějme S: Q = - 1 + 2 P; D: Q = 24 - 3 P; počáteční cena je rovna 3 jednotkám. Zpoždění je o jedno období na straně nabídky.
• Odhadněte intuitivně (pomocí porovnání sklonů S, D), zda je model konvergentní, tj. zda situace spěje k rovnovážné ceně.
• Jedná se o model nespojitý nebo spojitý?

Změna důchodu vlivem změny nabídky peněz.

• Pro výše zadanou ekonomiku zvol změnu nabídky peněz.
• Počítej dvěma metodami (multiplikátory, resp. průsečíky přímek)
• Řeš graficky (přesný nákres se změřením délek úseček).
• Výsledky porovnej. V případě neshody oprav.

Velikost vytěsněné produkce vlivem změny daňové sazby.

Urči velikost vytěsněné produkce vlivem snížení daňové sazby z hodnoty 0,25 na hodnotu 0,20.

• Ekonomika je popsána stejně jako v předchozím příkladě.
• Lze počítat oběma metodami jako v předchozím příkladě?
• Řeš také graficky (přesné zakreslení a ověření hodnot z grafu).
• Zapiš výsledky početního i grafického výpočtu symbolicky s využitím implikací (jako pravidlo). Došlo k posunu nebo otočení přímek v modelu IS-LM, a které.

Velikost vytěsněné produkce vlivem změny vládních výdajů

Urči velikost vytěsněného produktu vlivem fiskální politiky vlády v podobě zvýšení vládních výdajů o 100 jednotek. 

• Počítej pro autonomní spotřebu 100, mpc = 0,8; pro t = 0,25; transfery jsou ve výši 125 a vládní výdaje 400. L = 0,5.Y - 50.i; I = 300 - 30.i; nabídka peněz vztažená k cenové hladině je 500.
• Počítej dvěma metodami, a to (a) srovnáním multiplikátorů a (b) určením průsečíků přímek a jejich souřadnic důchodu. 
• Řeš také graficky (přesné zakreslení a ověření hodnot z grafu).
• Zapiš výsledky početního i grafického výpočtu symbolicky s využitím implikací (jako pravidlo). Došlo k posunu nebo otočení přímek v modelu IS-LM, a které.

Extrémní účinky fiskální, resp. monetární politiky

• Systemizuj všechny případy extrémní účinnosti fiskální, resp. monetární politiky. 
• Vždy zakresli obrázek, popiš účinnost na základě grafického vyjádření.
• Pro každý případ spočti účinnost na základě limity multiplikátoru.

Změna sklonu IS vlivem změny alfa

• Modeluj zvýšení daňové sazby analyticky a výsledek zakresli. Zapiš výsledek symbolicky.
• Modeluj zvýšení daňové sazby graficky a srovnej s předchozím výsledkem.
• Např. zvol autonomní výdaje 1 000; citlivost investic na úrokovou míru 40; mezní sklon ke spotřebě 0,8; výchozí daňovou sazbu 0,20; novou daňovou sazbu 0,25.
• První dva body zopakuj pro změnu mezního sklonu ke spotřebě (pro t = 0,20).

Změna sklonu IS vlivem snížení citlivosti investic na úrokovou míru

• Analyzuj početně i graficky pro AD = 1 000 + 0,7.Y - b.i, kde výchozí b = 40 a nové b = 5 (odvozujte vždy pro úrokové míry 10, resp. 5).
• Zapiš změny symbolicky.

Křivky IS, LM

• Urči závislosti IS, LM.
• Odvoď rovnováhu na trhu zboží početně, resp. graficky.
• Odvoď rovnováhu na trhu peněz početně, resp. graficky.

Sklon a posun LM (obecně)

• Co určuje sklon LM a vyvolává změnu sklonu LM? Odvoď a zapiš symbolicky.
• Co určuje posun LM a vyvolává změnu posunu LM? Odvoď a zapiš symbolicky.

Sklon a posun IS (obecně)

• Co určuje sklon IS a vyvolává změnu sklonu IS? Odvoď a zapiš symbolicky.
• Co určuje posun IS a vyvolává změnu posunu IS? Odvoď a zapiš symbolicky.

Změna sklonu LM vlivem změny k, resp. h

• Analyzuj početně i graficky pro k = 0,5; h = 0,75 a po změně k na 0,75, resp. h na 0,8.
• Zapiš změny symbolicky.

Vztah funkcí celkových a mezních

Která z křivek znázorňující Mf je správná???

Hledání extrémů funkcí dvou proměnných

Zopakuj si teorii pro hledání extrémů funkce dvou reálných proměnných

• (a) bez vazby, 
• (b) s vazbou
• extrémy funkcí jsou jednou z nejdůležitějších aplikací diferenciálního počtu

Pokles daňové sazby

• Ekonomika je dána těmito parametry: Důchod je 1000, mpc = 0,8, sazba důchodové daně se změní z 0,3 na 0,2.
• Popište rovnicemi AD před změnou a po změně.
• Danou změny AD zakreslete. Zobrazte změnu rovnovážné úrovně důchodu.
• Změnu důchodu kvantifikujte.
• O kolik se změní daňové příjmy vlády?

Spotřeba ve třísektorové ekonomice

• Je dána spotřební funkce C = 200 + 0,8 YD (disponibilní důchod).
• Investice jsou ve výši 100, vládní výdaje jsou 300, transferové platby 125, autonomní daně 100 a daňová sazba 0,25.
• Jaká je velikost multiplikátoru?
• Jaká je velikost celkové spotřeby?

Změna kvality vládních výdajů

• V ekonomice dojde ke snížení transferových plateb a současně ke zvýšení vládních nákupů zboží a služeb o stejný objem.
• Odvoďte teoreticky, jaký vliv má přesun na úroveň rovnovážného důchodu (modelujte rovnováhu před, resp. po změně; odečtěte). 
• Své úvahy ověřte výpočtem pro mpc = 0,8; t = 0,2; přesun vládních výdajů z položky transfery na vládní nákupy zboží a služeb je 50 jednotek. Jaká je změna rovnovážného důchodu.
• Na základě získaných znalostí popište současné intervence vlády a jejich důsledky (citujte z tisku a komentujte).

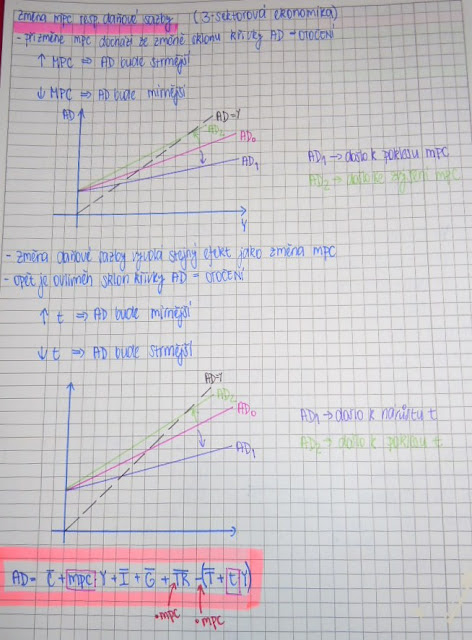
Změna mpc resp. daňové sazby

• Modelujte účinky změn mezního sklonu ke spotřebě, resp. změn daňové sazby (ve třísektorové ekonomice). 
• Popisujte a zakreslete.

Dvousektorová ekonomika

• Předpokládejme, že GNP = 1000 jednotek, přičemž C = 800 a I = 200, mpc = 0,5.
• Firma se rozhodne postavit sklad a její investice se zvýší z 200 na 210 jednotek.
• Popište přechod od staré rovnováhy k nové.
• Určete velikost přírůstku důchodu (odečtením dvou předchozích rovnic).
• Popište multiplikační účinek, tj. o kolik se zvýší GNP, když investice se zvýší o 10 jednotek.
• Zakreslete starou a novou rovnováhu, vyznačte změny I a GNP.
• Popište v obrázku multiplikační efekt.

Model pro maximalizaci ek. závislosti za omezení

Zopakuj teorie hledání maxima produkce při rozpočtových omezeních.
Zopakuj teorii hledání maxima investičních příležitostí při zdrojových omezeních.
Systemizuj formální analogie mezi různými ekonomickými disciplínami (tabulkou).

Maximalizace užitku řešení pro Klárku

Klári, tady je moje řešení tvého příkladu :)

Maximalizace užitku

• Připomeň si postup při hledání maxima užitku, resp. studuj z prezentace (Studijní materiály). Pokus se vysvětlit v modelu E3.
• Zvol své hodnoty ceny 1., resp. 2. výrobku, dále hodnotu důchodu spotřebitele (rozpočtové omezení) a funkci užitku. Své zadání zveřejni a vyzvi kolegu, aby hledal maximum užitku spotřebitele při rozpočtových omezeních, dále pak PCC a ICC, a zveřejnil je. Zašli komentář.
• Pokud nedojde ke shodě, otevřete konkrétní problém na cvičení.

Hledání extrémů funkcí 2 proměnných

• extrémy funkcí jsou jednou z nejdůležitějších aplikací diferenciálního počtu
• setkáváme se s nimi takřka všude
• ekonomické rozhodování se řídí požadavkem maximálního zisku a minimálních nákladů, přičemž tyto dvě veličiny často závisí na více proměnných
• rozlišujeme mezi extrémy lokálními, vázanými lokálními a globálními

Lokální volné extrémy (extrémy bez vazby)

1. parciální derivace funkce
2. parciální derivaci položíme rovnu 0, tím dostaneme stacionární body
3. derivace druhého řádu
4. vytvoříme determinant D
5. znaménko determinantu ve stacionárních bodech
6. znaménko druhé derivace ve stacionárních bodech

Lokální extrémy vázané (s vazbou)

1. vyjádření jedné proměnné z podmínky
2. dosazení do rovnice funkce
3. první derivace
4. první derivace položíme rovnu 0, tím dostaneme stacionární body
5. druhá derivace funkce
6. pokud bude druhá derivace menší než 0, je v příslušném bodě lokální minimum
7. pokud je druhá derivace větší než 0, je v příslušném bodě lokální maximum