Model pro maximalizaci ek. závislosti za omezení

Zopakuj teorie hledání maxima produkce při rozpočtových omezeních.
Zopakuj teorii hledání maxima investičních příležitostí při zdrojových omezeních.
Systemizuj formální analogie mezi různými ekonomickými disciplínami (tabulkou).

Maximalizace užitku řešení pro Klárku

Klári, tady je moje řešení tvého příkladu :)

Maximalizace užitku

• Připomeň si postup při hledání maxima užitku, resp. studuj z prezentace (Studijní materiály). Pokus se vysvětlit v modelu E3.
• Zvol své hodnoty ceny 1., resp. 2. výrobku, dále hodnotu důchodu spotřebitele (rozpočtové omezení) a funkci užitku. Své zadání zveřejni a vyzvi kolegu, aby hledal maximum užitku spotřebitele při rozpočtových omezeních, dále pak PCC a ICC, a zveřejnil je. Zašli komentář.
• Pokud nedojde ke shodě, otevřete konkrétní problém na cvičení.

Hledání extrémů funkcí 2 proměnných

• extrémy funkcí jsou jednou z nejdůležitějších aplikací diferenciálního počtu
• setkáváme se s nimi takřka všude
• ekonomické rozhodování se řídí požadavkem maximálního zisku a minimálních nákladů, přičemž tyto dvě veličiny často závisí na více proměnných
• rozlišujeme mezi extrémy lokálními, vázanými lokálními a globálními

Lokální volné extrémy (extrémy bez vazby)

1. parciální derivace funkce
2. parciální derivaci položíme rovnu 0, tím dostaneme stacionární body
3. derivace druhého řádu
4. vytvoříme determinant D
5. znaménko determinantu ve stacionárních bodech
6. znaménko druhé derivace ve stacionárních bodech

Lokální extrémy vázané (s vazbou)

1. vyjádření jedné proměnné z podmínky
2. dosazení do rovnice funkce
3. první derivace
4. první derivace položíme rovnu 0, tím dostaneme stacionární body
5. druhá derivace funkce
6. pokud bude druhá derivace menší než 0, je v příslušném bodě lokální minimum
7. pokud je druhá derivace větší než 0, je v příslušném bodě lokální maximum

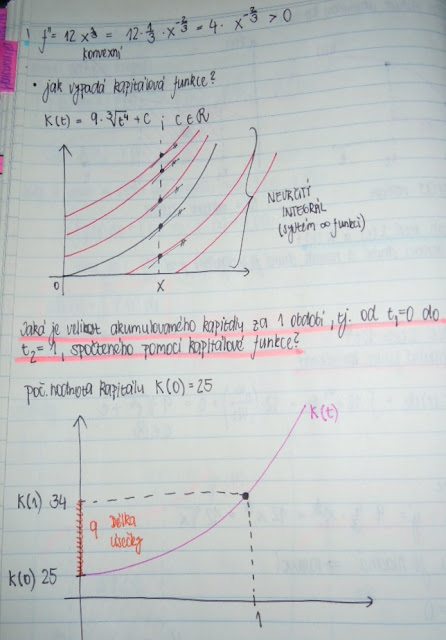
Akumulace kapitálu

• Nastudujte kapitolu z materiálu k samostudiu.
• Řešte příklad zadaný v materiálu k samostudiu. 
• Pokud potřebujete k danému tématu přednášku a cvičení, toto se bude konat po ukončení semestru pátým ročníkem.

Elasticita lineární, resp. kvadratické funkce

• Zvol lineární funkci a urči předpis její elasticity.
• Urči elasticitu ve zvoleném bodě početně, resp. graficky a výsledky porovnej.
• Totéž proveď pro funkci kvadratickou.

Funkce, kterou jsem použila pro demonstrování elasticity kvadratické funkce, není příliš vhodná. Tento příklad měl popisovat ekonomickou situaci, a tu daná funkce nepopisuje, protože se pohybuje v mínusových hodnotách. Nicméně jsem se tuto funkci rozhodla ponechat a v budoucnu zveřejním i příklad "ekonomicky reálný".

Paradox velké úrody, resp. Snížení poplatků za telefon

• Ukaž početně i graficky proč při velké úrodě sedlák pláče.
• Ukaž početně i graficky proč pláče žena, které se sníží poplatky za telefon.

Maximalizace zisku

• Urči maximum zisku, je-li: TR = 1 400 Q - 7,5 Q^2; TC = Q^3 - 6 Q^2 + 140 Q + 750. Počítej pomocí ekonomického pravidla, resp. matematickým postupem.
• Nakresli pod sebe 3 související grafy: 1. TR a TC, 2. zisk, 3. MR a MC. 
• Vyznač tečny ke grafům funkce TR a TC v bodě zvratu.

Hledání bodu zvratu

• Urči bod zvratu funkce TC: C(Q) = Q^3 - 12 Q^2 + 60 Q.
• Zakresli TC.
• Urči funkce MC a AC, zakresli do druhého (navazujícího) grafu.
• Vyznač tečnu ke grafu funkce TC v bodě zvratu a popiš její chování.
• Sleduj vztah funkcí MC a AC, a to v bodě zvratu a kolem něj.

Klikatka (ne hladká funkce)

• Zapiš definici hladké funkce.
• Zakresli svoji "klikatku", tj. funkci f spojitou, ale ne hladkou. Zvol alespoň 5 intervalů, při čemž v krajních bodech neexistuje derivace funkce f. Na každém intervalu zvol odlišný průběh funkce f - viz cvičení. 
• Pošli svou "klikatku" jako úkol spolužákovi a přijmi jinou od spolužáka.
• Do úkolu od spolužáka zakresli derivaci funkce f (do navazujícího obrázku - souřadnice si odpovídají).
• Úkoly a jejich řešení sdílejte přes webové rozhraní.
• Navzájem komentujte své výsledky.

Hladká funkce - funkce je hladká tehdy, a jen tehdy má - li spojitou derivaci.

Hledání extrémů funkce

Zopakuj si "kuchařku" pro hledání extrémů funkce jedné reálné proměnné.

• extrém je výjimečná hodnota, které nabývá hodnoty maxima nebo minima
• maximum je největší hodnota na dané množině
• minimum je nejmenší hodnota na dané množině

• Abychom tyto extrémní hodnoty našli, tak musíme nejprve zderivovat rovnici funkce.
• Tuto naši první derivaci funkce položíme rovnou nule a vypočítáme kořeny dané funkce.
• Kořeny funkce nazýváme body podezřelé z extrému funkce, protože mohou, ale také nemusí být extrémy funkce.
• V těchto bodech tedy můžou být extrémy, ale také se může jednat o inflexní body, proto se musí provést druhá derivace.
• Dalším krokem je dosazování. Do druhé derivace funkce musíme dosadit, body, které jsou podezřelé z extrémů funkce.
• Dále musíme výsledek vyhodnotit. Pokud bude výsledek dosazení do druhé derivace větší než 0, jedná se o lokální minimum. Pokud bude výsledek menší než 0, jedná se o lokální maximum.
• Inflexní body nalezneme tak, že položíme druhou derivaci rovnu 0 a vypočteme.

Příklad:

Progresivní a degresivní změny

Zakresli grafy funkce

• progresivně, resp. degresivně rostoucí 
• a progresivně, resp. degresivně klesající. 

Popiš vývoj sklonů jednotlivých funkcí.

Urči, kdy je funkce

• rostoucí s rostoucími sklony, 
• rostoucí s klesajícími sklony, 
• klesající s rostoucími sklony, 
• klesající s klesajícími sklony.

Sklon poptávky a nabídky

Mps a mpc

Spotřební a úsporová funkce a jejich mps, resp. mpc.
- Zakresli spotřební funkci a její sklon, vyznač souvislosti. Popiš.
- Zakresli úsporovou funkci a její sklon, vyznač souvislosti. Popiš.

Hladká funkce

Hladká funkce.
- Zvol si své dvě funkce, jednu hladkou a druhou ne, např. kvadratickou a s absolutní hodnotou.
- Ukaž, že funkce je, resp. není hladká, a to početně i graficky.

Tangens úhlu

Pro studium sklonu ekonomické funkce zopakuj vedle lineární a kvadratické funkce také funkci
     y = tg úhlu.

• Zakresli graf funkce.
• Vypiš vlastnosti funkce, které lze vyčíst z grafu. 
• Sleduj souvislosti mezi velikostí úhlu tečny ke grafu funkce v bodě, znaménkem funkční hodnoty a monotonií funkce (funkce restoucí, resp. klesající).

- tangens patří mezi goniometrické funkce

- grafem její funkce je tangenoida

Funkce , je definována jako
- definiční obor: 
- obor hodnot: 
- Rostoucí v každém intervalu

- Derivace: 

Derivace funkce

Vysvětli pojem Derivace (spojité diferencovatelné) funkce. Využij materiály, které najdeš, vkládej nalezené obrázky, texty, vkládej svá objasnění.

Derivace je základní pojem v diferenciálním počtu a má důležitou roli při určování průběhu funkce. Derivací funkce získáme směrnici tečny. Jednoduše řečeno, tečna je přímka, která se daného grafu dotýká právě v jednom bodě.

Na obrázku můžeme vidět černě znázorněný graf funkce y= X2 a modrá přímka je tečna k této funkci. Zeleně je vyznačen úhel α, který svírá tečna s osou x. Takže směrnice tečny je tangens úhlu, který daná tečna svírá s osou x. A tuto směrnici získáme právě pomocí derivací. Dále rozlišujeme pojmy derivace funkce v bodě a derivace funkce. Derivace funkce v bodě představuje právě směrnici tečny v daném bodě. Derivace funkce je pak jiná funkce, která předepisuje směrnice.

Pomocí derivace tedy umíme spočítat směrnice tečny.

Velmi důležité také je, že má-li funkce v bodě derivaci, pak je funkce v tomto bodě spojitá. Tento fakt vychází z vlastností limit. Pokud je ale funkce spojitá v daném bodě, neznamená to, že je zde zderivovatelná. Typickým příkladem je funkce f(x) = |x|. Graf je do špičky, nelze vypočítat směrnici tečny.